Moving from binary to ternary form, Nigel Scaife outlines the rich possibilities of an A-B-A structure with the help of a famous Prélude by Chopin
In Part 10 we began to look at binary form, using a simple but charming minuet by Mozart as our illustration. A piece in binary form has two sections, each of them usually marked with repeat signs. Each section of the minuet was eight bars long and the structure could be described in a diagram like this:

The theme of Bach’s Goldberg Variations is a classic example of symmetrical binary form in which the first A section ends with an ‘open’ cadence in the dominant. The B section, of equal duration, works its way back to end with a ‘close’ cadence in the tonic. There is much beauty in such well-crafted balance and sense of even proportion.
Sometimes this symmetrical structure is extended a little by a short codetta (from the Italian coda meaning ‘tail’). The opening Allemande of Bach’s French Suite No 6 is one example, which cadences back to the tonic four bars before its conclusion. These short codettas elaborate the tonic simply and round the piece off smoothly.
In other binary pieces the B section is much longer than the A section, perhaps twice as long or more, and passes through different keys before returning to the tonic at the end. The Menuet of the French Suite No 6 is a good example. This is known as asymmetrical binary form.

This two-part concept is extended further in many Baroque keyboard pieces such as dance movements within suites, or the self-contained sonatas of Scarlatti. It’s also encountered in shorter Romantic genre pieces by Schumann, Mendelssohn and others.
What might have been a short codetta becomes a more significant feature of the structure overall as it makes greater reference to the opening A section in the tonic. When this is the case it is usually called rounded binary form.
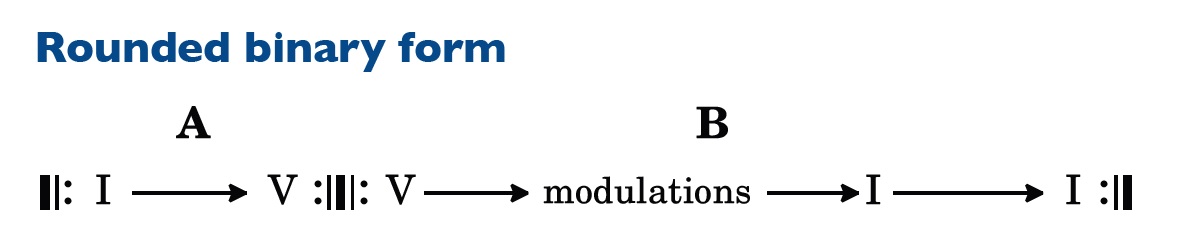
Such a form is clearly heading towards being more properly considered as a three-part structure and some theorists have preferred the term ‘incipient ternary’ to describe it. A piece in ternary form has three sections. In A-B-A the A sections are the same; in A-B-A the return of the A section is varied in some way. So while the two outer A sections use the same musical ideas, the B section – sometimes called an ‘episode’ – provides contrast and a sense of departure prior to the restatement of the original material in the tonic key.
The beauty of ternary form lies in the restatement of the main idea following a period of digression. This is a basic rhetorical concept found in music and language around the world. In a performance of a jazz standard, for example, the ‘head’ – the main theme heard at the start which is then subjected to variation and improvisation – is usually reprised at the end following a variety of solos.

Repetition of some kind – melodic shapes, rhythmic patterns or harmonic progressions – is generally thought necessary in order to bring cohesion to a piece. Without repetition it can be difficult to grasp the ideas on first hearing; the music may seem to wander aimlessly or to lack shape and balance.
On the other hand, too much repetition and the music risks becoming monotonous and dull. Composers may introduce formal contrast and variety with a new melodic idea, perhaps involving a modulation to a new key, or through changing the texture, the rhythm or the metre: the possibilities are endless!
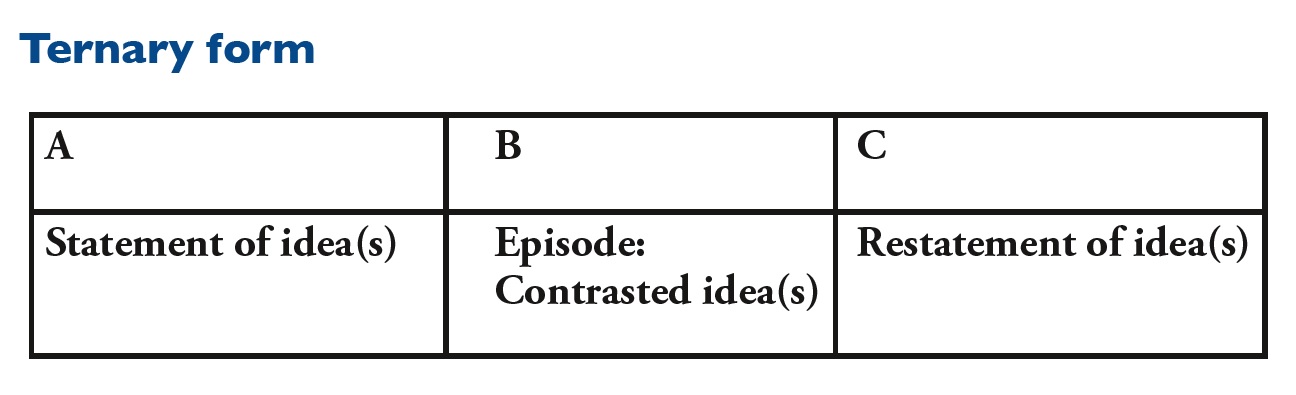
When the initial ideas are restated they can now be heard in a new light, viewed through the contrasting ideas of the B section. The restatement may be an exact repetition of the opening ideas or it may slightly varied, with some melodic embellishment or harmonic twist.
If the first section is to be repeated exactly then it is not necessary to have the music written out for a second time. In these cases the composer can use the Italian phrase da capo (often shortened to D.C.), meaning ‘from the start’ and the word fine – the end – will be written at the end of the A section.
The 'Raindrop' Prélude
Here is a classic example of ternary form, (Alfred Cortot’s poetic title for the piece was ‘Mais la Morte est là, dans l’ombre’ – ‘But death is here, in the shadows’ – which is perhaps more appropriate than the nickname derived from George Sand’s recollection of the work’s origins.) The opening section has a luminous theme which is dominated by a mesmerising Ab. This note acts as an inner dominant pedal point: it is the anchor for the entire prélude.
A pedal point is a note which is sustained through harmonic changes. The term derives from organ playing, as the organist is able to hold a note with a pedal while continuing to play moving parts on the keyboard ‘manuals’. The note that is sustained is very often the tonic or dominant and is usually found in the bass part. However, it may occur in an inner part, as in our Chopin example, in which case it is called an inner pedal, or occasionally it may be in the top part, in which case it is called an inverted pedal.
Sometimes two notes are sustained through harmonic changes, usually the tonic and dominant, and these are called, unsurprisingly, a double pedal.
Back to Chopin. The title of the prélude derives from this Ab pedal point, enharmonically changed to G# in the B section, and heard by many as an imitation of falling rain. Here is the famous opening idea:

The B section is full of foreboding, the death and shadows of Cortot’s imagination. From the Db major tonality of the A section there is a modulation to the tonic minor, now spelt as C# minor, and the melody has switched from RH to LH.
The contrast is stark and brings a dramatic change to the character of the melody. This B section is considerably longer than the outer sections and modulates through several keys, rising twice to impassioned fortissimo climaxes.
When the opening theme returns the septuplet in bar 4 is further embellished in an improvisatory way – a very Chopinesque feature. The theme is cut short and the pedal point is suspended for two bars. A single thread of melody begins an eight-bar coda in which dominant/dominant 7th and tonic chords are emphasised in a cadential fashion, bringing the prélude to a sombre resolution.

Considered purely in terms of bar numbers, the ternary form of this prélude is quite unbalanced: A (27 bars); B (48 bars); A1 (14 bars). However, many ternary-form pieces share this feature. One reason is that simple A-B-A forms are rare in folk and other kinds of popular song, which tend to be structured in verses of four rather than three or six lines.
Take the A-A-B-A form of The Ash Grove as an example:

I have written out this Welsh folksong with first- and second-time bars, in order to show that the tune divides into two parts. Does that make it a binary structure? Which is more important: equality of length, or repetition of melodic material? If you think the former is the most important aspect then it is a binary form, but if you think the latter then it is ternary.
However, the return of strong melodic material tends to make a greater impact than our awareness of the relative length of sections, so this type of structure is usually considered as ternary.
Harmonic structure also carries implications for form (and vice versa). The A section of The Ash Grove cadences on the tonic. It is a short but self-contained piece, whereas in a binary structure the A section usually modulates to the dominant and is therefore less able to stand on its own: it is dependent on the B section to return us to the tonic. In The Ash Grove the music modulates to the dominant at the end of the B section – here to D major, with the C# being harmonised by an A major chord (the dominant of D) followed by the tonic in a perfect cadence.
Different as they are, both the ‘Raindrop’ Prélude and The Ash Grove demonstrate the potential richness of a ternary structure. Idea – digression – restatement: there are so many possibilities within the form for creating both variety and unity.
Chopin’s Prélude in Db Op 28 No 15, ‘Raindrop’, is printed in the Scores section of Pianist 100.
Missed previous parts of the series? Check them out below:
About the author:
Nigel Scaife began his musical life as a chorister at Exeter Cathedral. He graduated from the Royal College of Music, where he studied with Yonty Solomon, receiving a Master’s in Performance Studies. He was awarded a doctorate from Oxford University and has subsequently had wide experience as a teacher, performer and writer on music.








