Music educator Nigel Scaife continues his exploration of intervals, discussing how the concept of consonance and dissonance is not the only way you can think of intervals...
Missed part 3 of the series? View it here
In part 3, we looked at how intervals are described and we covered all the intervals that are found in major and natural minor scales, starting from the tonic. If we take C major and C natural minor (with black note heads below), these intervals are as follows:

It is worth noting that a minor interval is always a semitone smaller than the corresponding major interval of the same number. So we have now covered the vast majority of intervals. But what about those that don’t form part of a major or natural minor scale? How can we describe the interval of C to F# or of C to Gb, as they don’t appear in either C major or C minor?
What about intervals that occur within major and minor scales that are as yet unaccounted for, such as this interval of a 4th which occurs in C major:

Using the method described in the last issue, where we take the lower note as a ‘pretend’ or ‘quasi’ tonic and work out the interval from that note, we have to consider this interval with the imagined tonic of F. It would be a perfect 4th but for the fact that the B is a natural and not the Bb in the key signature of F major. We’re going to need some new terminology! As this F to B natural interval is a semitone larger than the perfect 4th it is called an augmented 4th.
When any perfect interval is made a semitone larger it becomes augmented. The C to F# interval mentioned in my previous article is also an augmented 4th. Because this interval comprises three whole tones it also has the name tritone.
The tritone has a distinctive dissonant and unstable character. In medieval times the tritone was shunned as it was considered to represent the devil in music: diabolus in musica.
Let’s now look at the same interval and invert it – in other words, play the F above the B this time:

The notes B to F# would be a perfect 5th, with B as the imagined tonic.
However, as B to F natural is a semitone smaller than the perfect 5th it is called a diminished 5th. When a perfect interval is made a semitone smaller it becomes diminished.
For example, here are three types of octave:

This principle of diminished (reduced) or augmented (expanded) also applies to major and minor intervals. Look at the two middle examples below (b) and (c), which show intervals of a minor 2nd and a major 2nd.

In example (a) the size of the minor 2nd at (b) is reduced by a semitone, while the last example (d) expands the size of the major 2nd at (c) by a semitone. In reality, the diminished 2nd is not often used, because the notes of the interval are enharmonic equivalents:

However, the augmented 2nd often occurs as it is the interval between the 6th and 7th degrees of the harmonic minor scale:

Unisons, perfect 4ths, perfect 5ths and octaves are able to be diminished, perfected or augmented, and the same is true of 2nds, 3rds, 6ths and 7ths.
It is worth noting that an interval can be altered by changing the lower note, as well as by changing the higher note. Take for example this interval in the key of B minor:
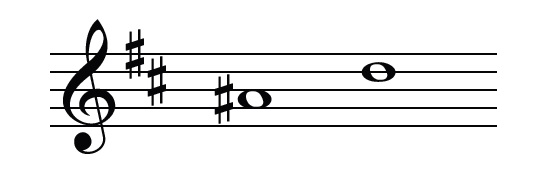
Had the lower note been an A natural, this would be a perfect 4th. But because the A is raised to an A#, making the interval a semitone smaller, it becomes a diminished 4th. When naming intervals it is often helpful to think of an interval of the same number that is easier to understand (for example, a perfect 4th) and then to adjust it to the actual interval (for example, a perfect 4th plus an additional semitone becomes an augmented 4th).
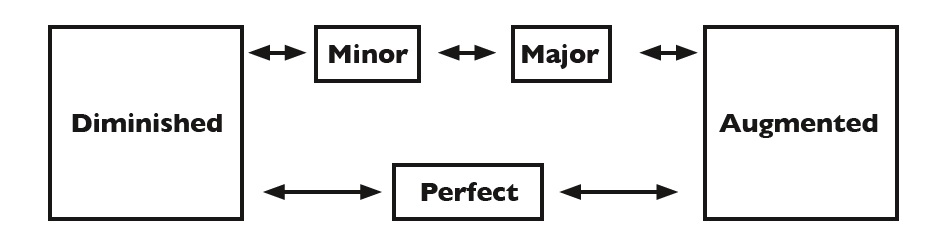
Here is a diagram showing the relationship between interval qualities. The arrows pointing to the right show the interval increasing by one semitone, while the arrows to the left show the intervals decreasing by one semitone:
Intervals that are larger than an octave are called compound intervals. They can be named in two ways:

In practice, musicians usually refer to a ‘9th’ or an ‘11th’ etc., rather than to a ‘compound 2nd or ‘compound perfect 4th’. The expression ‘compound’ can also refer to intervals greater than two octaves, so a compound 2nd can refer to the interval of a 2nd plus one octave or the interval of a 2nd plus two or more octaves.
For the last stage of our interval journey, we’re going to briefly consider an aspect that is crucial to the role of intervals as expressive entities and the way in which we hear them: consonance and dissonance.
The concept of consonance and dissonance, sometimes discussed in terms of concord and discord, is often compared with a state of rest versus unrest, or stability versus instability. An interval such as a major 3rd is said to be consonant because it sounds stable, while a tritone (augmented 4th) is said to be dissonant, as it gives a sense of tension which seeks a resolution.
The degree of consonance and dissonance in tonal music depends on context, as well as one’s own personal response to its expressive aspects. It is all rather subjective. Over the centuries opinion has varied as to what is considered discordant, but generally perfect intervals are considered consonant, along with major and minor 6ths, whereas major and minor 2nds and 7ths are considered to be dissonant, as are augmented and diminished intervals.
Dissonant intervals have varying degrees of discord in terms of their harshness, which is also subjective, but they tend to sound incomplete and in need of a resolution of some kind.
For example, listen to the effect of the tritone and the 6th on which it resolves in this example:

This sense of tension and release is at the heart of what makes music expressive. One of the classic examples of how to maintain a sense of suspense and a lack of resolution is found in Wagner’s opera Tristan and Isolde, where this famous opening sets the scene and creates a mood of longing and yearning through its ambiguity:

The first chord here is known as the ‘Tristan chord’ and is arguably the most famous chord in the whole of Western tonal music. Philosopher Bryan Magee has written that the Tristan chord ‘contains within itself not one but two dissonances, thus creating within the listener a double desire, agonizing in its intensity, for resolution. The chord to which it then moves resolves one of these dissonances but not the other, thus providing resolution-but-not-resolution.’ It takes virtually the length of the whole opera before the resolution is finally heard – but it’s worth the wait!
Rather than thinking in binary terms of concord and discord, it is more useful to think of this aspect of intervals as a continuum. Over time, as the conventions of the tonal system became increasingly under pressure from the chromaticism of the 19th century, as heard in Wagner, Strauss and Mahler for example, people’s perceptions of consonance and dissonance inevitably changed. The weakening of the tonal system during the 19th century led to what is sometimes called the ‘emancipation of the dissonance’.
That meant that intervals which were formerly considered dissonant could exist as self-standing entities which did not require a resolution. Instead they could be treated as though they were in fact consonant. This was certainly the case in the music of the Second Viennese School of composers, but also in the earlier music of Liszt, Debussy and a host of others.
The 4th is an interval that is less easy to categorise, as it takes on some aspects of being a perfect interval while also being considered dissonant. To some extent it depends where in the musical texture the interval occurs. The 4th is particularly effective when it clashes or conflicts with the underlying harmony and then resolves. When this happens it is called a suspension. Suspensions provide the main source of expressive dissonance in a lot of tonal music, especially music written during the Baroque period.
Typically, the note that is ‘suspended’ is found on a strong beat and is resolved on a weak beat. There are three parts to the process of suspensions.
Firstly, there is the preparation where there is a harmony note which is then held, often with a tie. Then there is the dissonance as the note is held, or suspended, against the changed harmony.
Finally, there is the resolution as the held note moves downward, resulting in a consonance. Usually the note of resolution is absent when the harmony changes, as in this example:

This is called a ‘4-3’ suspension, as suspensions are named by the number of the dissonant interval above the bass note (here D to G), followed by the interval of resolution. As well as 4-3 suspensions there are 9-8s, and 7-6s.
These can sometimes be heard in ‘chains’, when the resolution of one suspension forms the preparation note for another. This was a favourite device of the Italian Baroque masters such as Corelli and Vivaldi.
In part 5, we look at how chords are constructed, as well as how they are named using a variety of approaches.
Missed previous parts of the series? Check them out below:
About the author:
Nigel Scaife began his musical life as a chorister at Exeter Cathedral. He graduated from the Royal College of Music, where he studied with Yonty Solomon, receiving a Master’s in Performance Studies. He was awarded a doctorate from Oxford University and has subsequently had wide experience as a teacher, performer and writer on music.








