Being familiar with intervals will give you a greater understanding of what you’re playing, says music educator Nigel Scaife, who shows you how to differentiate a minor 6th from a perfect 4th...
Missed part 2 of the series? View it here.
Can you tell the difference between a major 6th and a minor 6th?
A diminished 5th from an augmented 4th?
How about a perfect 4th from a compound perfect 4th?
These questions may seem based on so much technical jargon and you may even be wondering – who actually cares? After all, you don’t need to know how to describe the distances between the pitches of two notes to play the piano or to appreciate music.
But that would be missing the point! Being able to describe the fundamental aspects of music (and you can’t get more fundamental than the way one pitch relates to another) is vital if you’re going to be able to talk and communicate about music in a meaningful way.
Having appropriate terminology gives you control over your sonic material and helps you to understand how music works – not just the rules of written notation but the ‘whys and wherefores’ that explain how music is put together and why it works in the way it does.
Understanding intervals is important when we consider the linear, melodic aspect of music as well as the vertical harmonic dimension. The distance between two notes that follow each other in a melody is called a melodic interval, while two notes that are sounded together simultaneously is, predictably, called a harmonic interval.
Measuring the distance of an interval is done by counting the notes from the bottom to the top. The most important thing to remember is that both notes must be counted. So a 5th above C is G and includes five letter names: C, D, E, F and G. Always count the lower note of an interval as ‘1’.
Here are all the harmonic intervals of the major scale starting on C:

The word unison is used instead of 1st. If two instruments play exactly the same note, or two people sing the same note, they are said to ‘in unison’. It may seem rather obvious, but it is helpful to consider the position of the intervals on the stave. The fact that both notes of 3rds, 5ths and 7ths always occupy either lines or spaces, or that octaves always have one note on a line and the other in a space, is particularly relevant when you are sight-reading, transposing or score-reading.
When counting intervals it doesn’t matter what type of notes, whether natural, sharp or flat are used. So any kind of C to G, such as C# to G# or Cb to Gb is still a 5th. Similarly any kind of C to F will be a 4th.
Take these two intervals:

We know that they sound exactly the same, but nevertheless the first interval is a 4th and the second one a 5th. This brings us to the different types of interval. Naming intervals by only using a number doesn’t give us a complete description. For example, the 5th from C to G is different in type from that of the 5th from C to Gb. So as well as using a number we need to define the distance between the pitches in a more sophisticated way using a descriptor that gives its quality as well as a number.
The most common types of interval are perfect, major and minor. These are the intervals that occur within the major and natural minor scales, as shown below. Note that the unison, 4th, 5th and octave are perfect in both scales, shown by the vertical lines in the diagram.
It is also worth noting that within the domain of intervals, the word major equals larger, while minor equals smaller:

The fundamental importance of the perfect intervals to the way our tonal system is organised can be related to the physical properties of sound. Without going into details of acoustics here, it is worth noting that it is these perfect intervals that form the basis of what is known as the harmonic series.
To demonstrate something of how the harmonic series works in practice, try this on the piano:

Once you have lifted off the left-hand octave you will hear the undamped strings of the right-hand notes giving their ‘sympathetic vibration’. A proper description of the harmonic series would be too much of a diversion here, but it’s a fascinating subject that is well worth exploring!
Let’s return to the major and natural minor scales and now place all their intervals in ascending order of size, again starting on C for ease. This gives us a different perspective on the intervals already covered.
From this we can more easily see that the minor intervals are always a semitone smaller than the major intervals of the same number:

There is one interval which we need to mention here for the sake of completeness: the minor 2nd. We’ve already seen from the diagrams above that a major 2nd is the same as a tone. The interval of a minor 2nd (which doesn’t occur in the natural minor scale) is the same size as a semitone, but it must be spelled using adjacent letters – so C to Db and not C to C#.
This is because it is always the letter names that are counted to find the number of an interval:
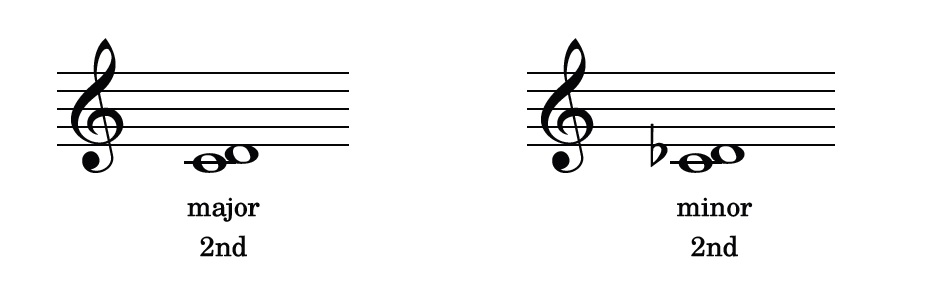
So far we have been naming intervals using the tonic in C major or minor as the lowest note, as this is the clearest way of describing them to start with. But what if the lowest note is not the tonic?
To work out the interval between any two notes, you have to imagine that the lower note is the tonic of either a major of natural minor scale. In both these scales the intervals between the tonic and the 4th, 5th and 8th degrees are always perfect. If the higher note appears in only the major scale of the imagined tonic, then the interval is major. With the exception of the interval of a 2nd, if the note appears in the natural minor scale, the interval is minor.
To illustrate this essential method of working out an interval, take the three bracketed intervals in this tune from Bach’s Partita No 5 BWV 829 in G major:

For the first interval, imagine F# as a tonic. We could start by thinking about F# major or minor, but given that F# minor has far fewer sharps (three, as it’s the relative minor of A major) let’s start there!
The note D is the sixth degree of the natural minor scale starting on F#, so this must be a minor sixth. In the second example imagine the lower note A as the tonic. In A major there is a C#, while in A minor the third scale degree is C natural, so this is a minor 3rd. The third interval is from D to F#. As the F# is the third degree of the major scale starting on D, this is a major 3rd.
To get intervals firmly established in the mind’s ear as discrete entities which are immediately recognisable, many teachers use the start of well-known songs as a kind of aide memoire or a way of double checking.
Here are some typical examples where the intervals are ascending but you can, of course, think of your own favourites and also find alternatives where the interval is descending:
- Minor 2nd The Pink Panther
- Major 2nd Happy Birthday
- Minor 3rd Greensleeves
- Major 3rd Morning has broken
- Perfect 4th Amazing Grace
- Perfect 5th Scarborough Fair
- Minor 6th Chopin Waltz op 64 no 2 in C sharp minor
- Major 6th My Bonnie Lies Over the Ocean
- Minor 7th There’s a Place for Us (West Side Story)
- Major 7th Bali Hai (South Pacific) (1st & 3rd notes)
- Octave Over the Rainbow
We have now covered the majority of intervals. In the next article we will look at how intervals such as those on the previous page (e.g. C-F#/Gb) are described, as well as intervals which are larger than an octave.
Nigel Scaife continues the series with Part 4, which you can view here.
Missed previous parts of the series? Check them out below.
About the author:
Nigel Scaife began his musical life as a chorister at Exeter Cathedral. He graduated from the Royal College of Music, where he studied with Yonty Solomon, receiving a Master’s in Performance Studies. He was awarded a doctorate from Oxford University and has subsequently had wide experience as a teacher, performer and writer on music.








